公共経済学06: 間接税のラムゼイルール

ラムゼイルール（最適な物品税・消費税の税率についての理論モデル）、物品税は需要の価格弾力性の逆数に比例するという逆弾力性の命題も導出しました。
　最適課税理論では、必要とされる税収  を確保しつつ、税によって生じる超過負担・死荷重を最小化することが多いです。価格ベクトルを  とすれば、物品税を課すということは要するにこの価格を（課税によって）動かすこと。したがって、政府にとっての最適化問題は次のようになります：
　 
制約式は、税収  が必要とされる金額  を下回らないこと。目的関数  は、代表的家計の間接効用関数。これを最大化するということは、必要な税収をあげつつ家計の効用水準を最大化することなので、要するに、超過負担・死荷重を最小化することに等しいわけです。
　この最大化問題をとくことで、ラムゼイ・ルールを得る。特に、交差価格弾力性がゼロであるという特殊かつ簡略化された仮定のもとで最適税率に関して次式を得る。
         
 は所得の限界効用  で、  はラグランジュ乗数、  は  財需要の価格弾力性。   財への消費税率は、その財の価格弾力性に反比例する。すなわち、消費税（物品税）を決めるときは、「価格弾力性の高い財（たとえば贅沢品）には低い税率で税をかるく、逆に、価格弾力性の低い財（たとえば必需品）には高い税率をかける」ことによって、税によるゆがみ・効率性損失を最小化できるという教えが導かれます。もちろん、ここでは、税のゆがみを最小化したい場合の解なので、公平性の問題はいったんはずしてかんがえています。贅沢品にかるく、必需品におもい消費税は、「金持ち優遇」として批判されうるし現実的ではありません。実際には、食料品などの必需品には軽減税率（低い税率）が適用されることが多いはずです。

練習問題


1) 次の効用関数をもとに最適な物品税を導出してみよう。まず間接効用関数を出して、それを上の最大化問題に代入して解いてみよう。
  ,
  ,

交差弾力性はゼロにしてあるが、うまく逆弾力性命題は導出できるだろうか。

2) 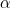 は所得の限界効用。  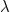は限界的な減税の限界効用。計算していくと、どうやら、後者のほうが大きくなるはずだ。どういうことだろうか。

3) 2財モデルで図を描く。税が課せられる前の予算制約線（赤）に無差別曲線が接している図を描き、その接点をA点としよう。ここで、縦軸のy財だけに課税したとしよう。課税後の予算制約線（y切片だけが原点のほうに動いたもの、緑）に無差別曲線が接するように、家計は消費バンドルを選ぶはずだ。その接点をB点としよう。A点とB点の距離が税額・税収になるはずだ。

　で、課税前の予算制約線と平行で、かつ、B点を通るような予算制約線（紫）を考えよう。その新しい予算制約線と無差別曲線の接点をC点とする。標準的な無差別曲線を描き、効用水準を比較すれば、A点＞C点＞B点となる。さて、C点を家計が選んだときの税額も、B点を選んだときの税額も、等しくなる。したがって、C点を実現させるような課税の方法が、Y財だけに課税するよりも望ましいということになる。C点を実現させるような課税とは、各財に均等に税率を課すものであり、ラムゼイルールのように需要の価格弾力性に応じて税率を調整させるようなものではない。

　さて、このモデルとラムゼイルール、どちらが正しいのだろうか。なぜ、結論がちがってくるのだろうか（あるいはちがっているように見えるのだろうか）。