実験経済学8：リスク選好・アレのパラドクス

アレのパラドクスを、さらに２つのやり方で実感してみる。ひとつは、別のギャンブルをひとつだけ用意して、そのギャンブルでの意思決定を考えることで、パラドクスがよりわかりやすくなるというもの。もうひとつは、Machina-Marschakの三角形で、再度、アレのパラドクスを図解してみました。宿題が出ていますので、コースナビを必ずチェックしてください。

基礎ミクロ22：価格あたりの限界効用 リスク・保険

予算制約つきの効用最大化問題を解いたときに（max u(x,y)）、最適解において、ｘ財の限界効用をｘ財価格で割ったものと、ｙ財の限界効用をｙ財価格で割ったものが等しいはずだ。この意味をヒューリスティックに考えました。

つづいて、教科書第１４章の３３２～３３４ページの図を勉強しました。

基礎ミクロ21：『女工哀歌』

女工哀歌 [DVD]

『女工哀歌』というドキュメンタリー映画を視聴。メイド・イン・チャイナの安い商品（ここではジーンズ）を作っている工場での日常を、そこで働く少女の視点で描いています。時給７円(!)で、休みなく昼夜延々と働く工員たちの暮らしぶり。お湯も出ない、シャワーなんてない寮の部屋に寝て、となりの工場で早朝から深夜まで働く少女たち。

中国の奥地にいけば、時給７円で１日１２時間以上働いてくれる労働力が豊富にある。フリーター問題・ワーキングプア問題、あるいはグローバル経済を考えるときに、見逃せない事実でしょう。邦題は、もちろん『女工哀史』からとったもの。大正１４年、日本もまだまだ貧しかった。



この本では、「万人が生きるがためには、彼女[女工]を犠牲にせねばならぬという法は断じてあり得ない。」そして、この解決には搾取する資本家（働かざるもの）も働かねばならぬのであって、「...各人が義務服役をなすのである。ここにおいて...当然"工場国有"が実現するであろう。」としている。うーん、だが残念ながら、これが"寝言"であったのは歴史をみればわかること。一筋縄にはいかない。

基礎ミクロ20：「無差別原則」

『ランチタイムの経済学』第４章に載っている「無差別原則」について話しながら、均衡のイメージをつかみます。一般均衡を勉強したあとだったので、経済モデルに現実性がなくとも、そのエッセンスを無視することはできないことを考えました。この本のトーン、道徳の揚げ足取りのような態度は好きではないのですが、経済学モデルを考えるにあたってはとても良い副読本だと思います。


「経済なき道徳は寝言、道徳なき経済は犯罪」。経済学（者）は前者を強調するきらいがあるが、後者も忘れないでください。

実験経済学7：リスク選好・アレのパラドクス

確率的に結果が変わりうるときに、どのように意思決定をするのかを考えます。事前に計算できる金銭的利益の期待値を最大化するべきなのか、金額を効用関数のようなフィルターを通して、その上で期待値をとるのか、などなど。

ところで、コイン投げを１００回繰り返すと、表は何回でるのでしょうか。「５０回」と即答してしまいがちですが、それはあくまでも"平均的に考えたら"ということ。表がちょうど５０回でる確率は、実は８％弱しかない。つまり、１００人を集め、各人にコイン投げを１００回してもらい、「表がちょうど５０回出た人、手をあげて」と聞くと、だいたい８人ぐらいが手をあげて「５０回出ました」と報告してくる。他の人はみんな、５１回出たり、あるいは４７回しか出なかったりということ。

さらにいえば、この「１００人同時コイン投げ実験」をしたときに、そのうちの８人が「ちょど５０回出ました」と報告してくる確率も事前に考えることができたりする。
で、表が出やすい歪んだコイン（表がでる確率がすこし高い）を考える。いま手元にあるコインが歪んでいるのか否か。断定的な結論を出すことはできないが、統計的にある一定の確率で間違っているかもしれないけど、どうやらこのコインは歪んでいるんじゃないか、とは言える。これがよく聴く「統計的に有意だ」と説明。

話を戻して、アレのパラドクスを説明しました。詳しくはまた次回。

基礎ミクロ19：パレート効率性・厚生経済学の基本定理

エッジワースボックス（２人２財の交換経済）で、パレート効率性・均衡価格・厚生経済学の第１基本定理の意味「市場均衡での配分はパレート効率的だ」を確認しました。そしてメッセージは、２人２財を拡張して考えれば、市場機構・価格機構が、いわゆる「クラウド」のイメージなんだということでしょう。


まず、太郎と花子の間の物々交換の話であったところに、あえて貨幣を導入します。物の値段というのは、その商品と１円玉との交換比率であるわけだけど、実は、２財（りんごとミカン）の値段を比べることで、その２財を仮に物々交換するとすれば、そのときの交換比率がいくつになるのかも間接的に規定しているわけです。物価体系→物々交換比率ということ。じゃ逆に、物々交換比率→物価体系というストーリーも考えられる。そこで、太郎と花子の間の物々交換を、太郎―市場―花子のように考え、各個人は市場と取引しているとみなしてみる。

太郎も花子もプライステイカーだと想定するので、いずれも、市場に提示されたりんご・ミカンの値段をみて、自分の「予算」の範囲内で効用を最大化するようにりんご・ミカンを需要します。ここで注意したいのは、市場が提示した価格に応じて太郎・花子が需要した量が、供給量（＝社会に存在するりんご・ミカンの総量）に必ずしも一致しないということ。（需要量と総量が一致している図をいきなり描いている教科書も少なくないけど、あれはミスリーディングだと思います）。問題はなにかといえば、りんごorミカンが足りないこと。そして、足りないというのは、需要が多すぎるということ。（ややこしい話はおいておけば）、需要が多すぎるというのは、それが安すぎるからだろう。価格比が別のものならば、需要と供給は一致するかもしれない。

そこで、均衡価格の定義に戻れば、需要の合計と、供給量（＝社会に存在するりんご・ミカンの総量）が一致するような価格比があるはず。うまく図を描くことができればOK。「市場均衡での配分は、パレート効率的だ」という厚生経済学の第１基本定理（のエッセンス）も確認できます。


余談：文章の書き方を中等教育でも大学でもろくに教えてくれない。大学受験の問題設定がそれを前提としていないからでしょう。たとえば、パラグラフにはトピックセンテンスを１文いれることを習ったことがあるというのは、本当に数人だけでした。ということで、木下是雄『理科系の作文技術』中公新書を紹介しました。秀逸。

基礎ミクロ18：エッジワースボックス

第８章のボックスダイアグラムの書き方・読み方。そして、契約曲線、パレート最適といった概念を勉強しました。

実験経済学6：公共財供給実験

公共財供給実験の結果について勉強しました。複数人で１組となり、各自が自分の初期の持ち点のうち、いくらかを拠出して公共財を作り、その便益を全員が均等に享受するというゲームです。利己的に振舞えば、公共財への拠出はゼロとするのが最適となるように利得構造が仕組まれています。それでも、完全に利己的な振る舞いをする人は少ないです。しかし、「経済学者はタダ乗りをする―――他に誰がするというのか？」という刺激的なタイトルの論文があり、合理的（利己的）思考になれた（あるいはそうした意思決定しかできない性格の人が多い）経済学者だけは例外で、経済学部の大学院生の拠出額が際立って低いことが示されています。

ともかくも、どういった要素が人々の拠出額に影響を与えるのかを探るために、あらゆる実験が行われてきました。同じゲームを繰り返すと拠出額は下がってきます。また、参加人数を増やしてタダ乗りの罪悪感を和らげたり、同じゲームを繰り返すものの、メンバーを入れ替えたり・入れ替えなかったり、etc。

基礎ミクロ17：所得効果・代替効果、労働供給

第６章残りと、第７章を勉強しました。労働の供給曲線を描くと、それが必ずしも右上りにならない背景について、十分に理解していただければ第６章はOKです。第７章では生産技術に関しても、無差別曲線と同じようなものを描くことができ、費用最小化問題を考えることができることを勉強しました。

さらに、ある一定量の財を生産する場合、もし社会全体での資源・費用を最小化するならば、各生産者の限界費用が等しくなっているはずだということを見ました。一方、市場では、各生産者が利潤最大化する結果、価格＝限界費用となる水準まで生産するはずです。すると、市場で各生産者が利己的に行動しても、実は、フタを開けてみれば、社会全体での総費用が最小化されているのだということにもなります。

基礎ミクロ16：『誰が電気自動車を殺したか』

市場の動きと、資本の動き、政府の動き。それぞれを考えるのに、いい材料です。

誰が電気自動車を殺したか? [DVD]

基礎ミクロ15：価格変化と消費行動

ラグランジュの未定乗数法を復習してから、教科書第６章の第１節を勉強しました。

半径Rで、高さｈの円柱形の缶詰を考えて、以下２つの別のアプローチをとる。１．表面積（＝缶をつくるのに必要な金属の量）に上限があって、その制限内で容積を最大化するように缶のサイズを設計するという問題、２．最低限Vだけは容量を確保するという制限があり、その缶に使用する金属の量を最小化する問題。

教科書では、予算制約を動かしながら、無差別曲線との接点がどのように動くのかを考えました。

実験経済学5：公平性（最後通牒ゲームと独裁者ゲーム）

公平性は、経済学のなかでも、現実の経済現象や経済的意思決定を考えるうえでも、重要です。ここでは、最後通牒ゲームと独裁者ゲームの結果を比べ、公平にみえる行為と利他的動機などについて考えました。公平性をそのまま効用関数に組み入れれば、不平等回避を加味した利得関数ができあがり、その不平等回避の強さを表すパラメーターを推定することができます。次にするべきなのは、そうして作った新しいモデルと推定したパラメーターで、異なる環境での意思決定を同様に説明できれば、モデルに意味はあります。

最終的な利益だけを単純に利得関数にいれるのは、プロセス（どうしてその利益を得るにいたったか）を重視しない、いわば帰結主義的なアプローチです。現実には、プロセスを重視して人々は意思決定しているので、非帰結主義的な評価をしているはず。たとえば、クイズを事前にやって、そのクイズの高得点者を提案者にしてあげるような場合。このケースでは、提案者の取り分が多くなることについて、提案者と（クイズの得点が低かった）受け手の間には、暗黙の合意が成り立つようです。あるいは、別の選択肢があって、１）公平な分配提案をできるにもかかわらず不公平な(8:2)を提案してきたとき、と　２）もっと不公平な提案ができたにもかかわらず不公平な(8:2)を提案してきたとき、とではん、(8:2)を受け手が拒否する頻度は大きく変わります。

基礎ミクロ14：予算制約下での効用最大化問題

ｘ教科書にはないところを勉強しました。次のような、2財モデルでの効用最大化問題を考えてみましょう。

　.

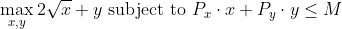予算Mの範囲内で、x財とy財を購入し、そこから得られる効用を最大化するという問題です。３つのアプローチで解きました。ちなみに、高校数学の範囲で十分解けるはずの問題です。

１つ目は、予算を使い切ることを前提に予算制約式から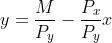 を求め、それを効用関数に代入する方法。あとは、それをｘについて微分したものが、最適な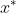において、ゼロとなるはずだから、その等式より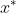が求まります。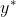も予算制約から求めます。

２つ目は、前回の講義で勉強したように、効用を最大化する最適な消費点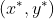 において、無差別曲線と予算制約線が接する性質を使います。無差別曲線は 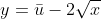なので、そのx-y平面における傾きは 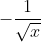。一方、予算制約線の傾きは、 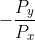。これらを等号でつなげばいいのです。

3つ目は、ラグランジュの未定乗数法と呼ばれるときかたです。こちらが本題でした。解法と、ラグランジュ乗数の解釈について、実際に計算して確かめました。

詳しくは、以下の148頁あたりをご参照ください。品切れなので、148頁～149頁だけを受講生のみなさんに配布する予定です。書籍化されるかもしれませんので、そのときぜひ購入しましょう。

経済学で出る数学 高校数学からきちんと攻める 2008年 10月号 [雑誌]

基礎ミクロ13：無差別曲線と予算制約

教科書Part2の一般均衡分析にうつり、今日は第5章を終えました。無差別曲線と予算制約下での効用最大化を勉強しました。「無差別曲線の性質」として、交差しない、右下がりだ、原点に対して凸だとか書いてありますが、それらはあくまで仮定にすぎません。実際の無差別曲線が必ずしもこうした「性質」を満たしているとは限らないので、性質という言葉遣いはミスリーディング。あくまで「（この）教科書で扱う無差別曲線の特徴」という意味にすぎない。経済学というアプローチのなかでとられる一般的想定にすぎません。

演習問題２を各自やっておいてください。

以下の本を紹介しました。学生時代を有意義に過ごすためのヒント。大学生活本はあまたあるが、たいていは読みにくい。この本は大変読みやすく、インタビュー実例もたくさんあり、良書です。

就活難民にならないための大学生活30のルール
常見 陽平

実験経済学4：サンクトペテルブルクのパラドクス

さて、このゲームでは、コイン投げをして、表がでれば、コイン投げを続けることができます。裏がでた時点でゲームは終わりです。ゲームが終了するまでに、何回（連続して）表が出たかによって、何本のうまい棒がもらえるかが決まります。いきなり裏が出てしまった場合（表が０回のとき）は、うまい棒が１本もらえます。表が１回だけで次に裏が出てしまったら、２本もらえます。表２回で３回目に裏が出てしまった場合は、４本だけもらえます。このように、連続して出た表の数が１回増えるごとに、ゲーム終了時点でもらえるうまい棒の本数が２倍に増えていくのです。問題は、このゲームに一体いくら払って参加したいか（参加するのにいくらまでなら払いますか）ということ。実際に、一橋大学の学生さん１２５人に聞いてみた結果が右のグラフにある通りで、平均５４円でした。

ここにパラドックスがあります。実は、理論的には、このゲームの参加費は無限大になってもおかしくないからです。ゲームの参加費を決めるときには、おそらく、「このゲームに参加すれば何本ぐらいのうまい棒が平均してもらえるのだろうか」と考えたことでしょう。ゲームに参加すれば、少なくとも１本のうまい棒はもらえるはず。それよりも多くうまい棒をもらうためには、少なくとも１回は表が出ればいいのだから、確率５０％で、２本以上のうまい棒がもらえます。というように考えて、平均何本もらえるかを何となく予想するはずです。計算自体は簡単ですので過程を省きますが、驚くべきことに、平均してもらえるであろう本数は無限大となってしまうのです。だとすれば、ゲームに参加することには無限大の価値がある！？　となります。感覚的にも、とてもそれには納得がいきませんし、学生さんが答えた平均５４円という数字をどのように解釈すればいいのでしょう。

５４円という数字を解釈するひとつの方法が「効用」という概念の導入です。人はうまい棒の本数だけにもとづいて判断するのではなく、そのうまい棒が自分にとってどれだけの価値があるか（それによってどれだけの満足度（効用！）が得られるか）を考えているはず。そこで、うまい棒ゲームでもらえるうまい棒を消費し、その消費から得られる効用の平均値（期待値）を計算するのではないかと思えます。実際に、得られる効用をうまい棒の本数の対数関数 log(x) として、効用の平均値を計算すると、それは無限大にならないことがわかります。

この log(x) という関数はヴェーバー‐フェヒナーの法則にうまく対応しています。刺激の物理量と、人がそれを知覚する強さは比例関係ではなく、対数比例しているという法則です。講義では、117番の時報を聞いてもらいました。時報の「ピピピッピーン」はラの音で、はじめの３つが基準音で、最後のッピーンが1オクターブ高いラの音。前者が440ヘルツ、後者は880ヘルツで周波数が２倍。さらにオクターブ上がれば、２倍の1760ヘルツなんだそうです。周波数（物理量）が２倍になるごとに、人はそれを１オクターブあがったものと知覚します。オクターブのピッチは、人にとって倍数ではなく、等間隔でしょう。これを表すのが対数関数です。

消費量（物理量）と効用（感覚量）についても同じように考えてもいいでしょう。うまい棒の本数（物理量）が増加しても、その効用（感覚量）は比例して増加するわけではありません。むしろ、ヴェーバー‐フェヒナーの法則にしたがえば、うまい棒の本数が２倍になるごとに、その効用は同じ絶対量（水準）だけ増加するということになります。つづきは講義スライドをごらんください。